4. Calculando números que informan sobre los datos
Antes de continuar, te vamos a preguntar una cosa. Si sacas en dos exámenes un 8 y un 6, ¿a que sabes tu nota media? Lo que haces, quizá sin saberlo, es sumar las dos notas y dividir lo obtenido por dos ¿verdad? Eso que haces se llama media aritmética.
Te vamos a contar más sobre ella y sobre alguna otra cosa… y haremos algunas cuentas
La media aritmética
Importante
Se llama media aritmética de una variable aleatoria a la suma de todos los valores observados dividida por el total de observaciones.
Volvamos al ejemplo del desayuno:
Hay dos formas de calcular la media artimética. Una "a lo bruto" y otra "pensando un poco":
- A lo bruto: sumamos todas las respuestas que nos han dado los vecinos y dividimos entre los 10 vecinos encuestados:
(0+0+9+0+5+5+9+5+15+0):10 = 48
48:10 = 4,8
Esto quiere decir que si todos los vecinos desayunasen el mismo tiempo, desayunarían todos 4,8 minutos.
- Pensando un poco: ¿y si en vez de sumar los valores como antes primero multiplicamos cada valor por las veces que se repite? Es decir: en la suma anterior hay, por ejemplo, tres cincos… ¿no sería mejor poner 15? Y así con el resto.
En realidad lo que haríamos sería sumar cada valor multiplicado por su frecuencia absoluta y dividir después por el número total de observaciones:
(0·4 + 5·3 + 9·2 + 15·1):10 = 48:10 = 4,8 minutos.
Podemos usar la tabla de frecuencias para este cálculo.
Ahora piensa: aunque hay un vecino que tarda en desayunar 15 minutos… ¿crees que los vecinos pasan bastante tiempo desayunando?
Curiosidad
Fotografía en Flickr de Olga Berrios . Licencia cc |
¿Qué ocurriría si…?
¿Qué ocurriría con la media anterior si un vecino tardase dos horas en tomarse su café y sus tostadas?
A la suma anterior tendríamos que añadir 120 minutos y obtendríamos 168, ahora dividimos entre el número de vecinos encuestados (que serían 11) y... SALE UNA MEDIA DE MÁS DE 15 MINUTOS.
¡Ya quisieran los demás tener tanto tiempo para desayunar! Se ha triplicado la media anterior.
Como ves, los "valores extraños" pueden producir medias extrañas que no reflejen realmente la realidad.
Caso práctico
Un caso especial:
¿Cuánto vale la media si todas las respuestas son iguales? Piensa un poco.
Por ejemplo, si todos los vecinos hacen el mismo número de comidas diarias (4), la media de comidas diarias es justo eso, 4 comidas.
¡Haz la cuenta y verás que no es magia!
Moda
 |
Icono en Pixabay. Licencia CC0 |
¿Qué quiere decir que un color está de moda? Pues que la mayoría de la gente se viste con ese color. ¿Qué significa que está de moda desayunar cereales? Que la mayoría de la gente toma cereales…
Y así podemos seguir.
¿Qué será la moda de una variable estadística?
Efectivamente, acertaste
Importante
La moda de una variable estadística es el valor más frecuente, el más repetido en las respuestas… el de mayor frecuencia absoluta (o relativa).
Rellenar huecos
Curiosidad
Piensa un momento
¿Crees que puede haber más de una moda en una variable estadística?
Te ayudamos a pensarlo con una pequeña pista: sacude tu memoria… ¿te suena esto?
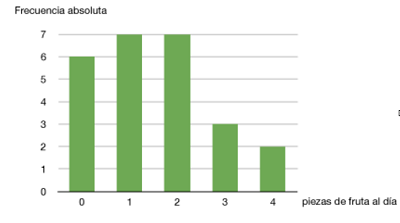 |
| Imagen elaboración propia |
Efectivamente, puede haberla. Observa en la gráfica que hay dos valores con frecuencias iguales y ningún otro valor es más frecuente; ambos serán moda. Así podemos tener variables unimodales (con una moda), bimodales (con dos modas, como en el gráfico)...y hasta polimodales o multimodales (con varias modas).
Si la variable está agrupada en intervalos, podríamos indicar el intervalo modal (el intervalo que más datos "contiene").

Comentarios
Publicar un comentario