A esa operación se le llama producto de un escalar por un vector.
Expliquemos con la siguiente imagen las operaciones que podemos hacer con los vectores:
Vuelve a mirar en la infografía de arriba el segundo caso, el de fondo amarillo. El vector tiene el mismo módulo y dirección que el original, pero sentido contrario. Es lo que se denomina vector opuesto
¿Tienes claro qué es un vector opuesto?
Pues un ejemplo son las fuerzas que realiza el personaje de la imagen con cada uno de sus brazos (misma dirección, mismo módulo pero sentidos opuestos)
 |
Si sumamos vectores con la misma dirección y sentido, el resultado es un vector con dicha dirección y sentido y cuyo módulo es la suma de los módulos de cada uno de los vectores.
¿Y qué sucede cuando los sentidos son opuestos?
Los dos animales de la imagen están luchando. Intervienen muchas fuerzas. Vamos a simplificar la crítica situación centrándonos en sus cornamentas. Sus cabezas ejercen fuerzas en la misma dirección pero en sentidos opuestos. Ganará el animal que más fuerza (módulo) ejerza.
Vas a repasar cómo se calcula suma de vectores en los distintos casos
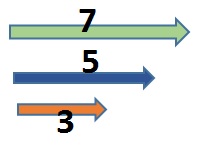
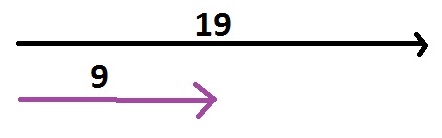
1.Calcula la suma de estos vectores (la cifra indica su módulo)
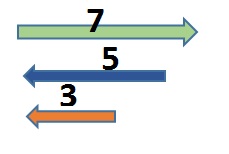
2. Ahora vas a calcular la suma de los siguientes vectores:
|
Estamos ante el caso de vectores (en este caso fuerzas) con distinto módulo (aunque podrían ser iguales), misma dirección y distinto sentido.
En las siguientes infografías se explica.
 |
¡Se puede complicar todavía más!
Las situaciones que se dan en la vida real, en ocasiones, son mucho más complejas.
Imagínate todo este grupo de personas remando para no volcar y cada cual ejerciendo una fuerza con su remo donde mejor le parece. Y no olvidemos el agua con su lío de corrientes.
¿Cómo sumamos todos esos vectores (en este caso fuerzas)? En las siguientes infografías se explica.
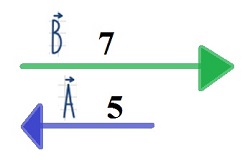
1. Fíjate en los vectores de la imagen. La cifra indica su módulo
|
¿Cuál de los siguientes vectores es el resultante de la operación 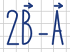 ?
?
|












Comentarios
Publicar un comentario